Connecting to the Gertboard

So while the Gertboard has LEDs and buttons, it’s really intended to be used to safely connect the Pi to external devices, and to do this we need to look closer at what it provides.

There are 12 buffered pins – these can be individually configured as inputs or outputs. As inputs they take a maximum of 3.3v and as outputs they can source (or sink) a maximum of 20mA each.

Additionally, there are 6 outputs that go to a ULN2803A darlington driver chip. These (open collector) outputs can sink a maximum total current of 500mA. They can be used to drive relays and small motors and small incandescent bulbs.

As well as the 12 buffered pins and 6 higher power outputs, there is a motor driver which is capable of driving a DC brushed motor forwards, backwards or at a variable speed using PWM and there is also an analog to digital converter and a digital to analog converter. We will look at all these in turn.

The buffered input and output pins

These pins are really extensions of the Pi’s own GPIO pins – however they are passed through the 72×244 buffer ICs. This is to act as a protection for the Pi – cheaper to blow up one of these chips than your entire Pi…

They can drive other 3.3v logic devices, small LEDs and sense switches, but remember that they are limited to an input voltage of 3.3v, and an output current of 20mA.

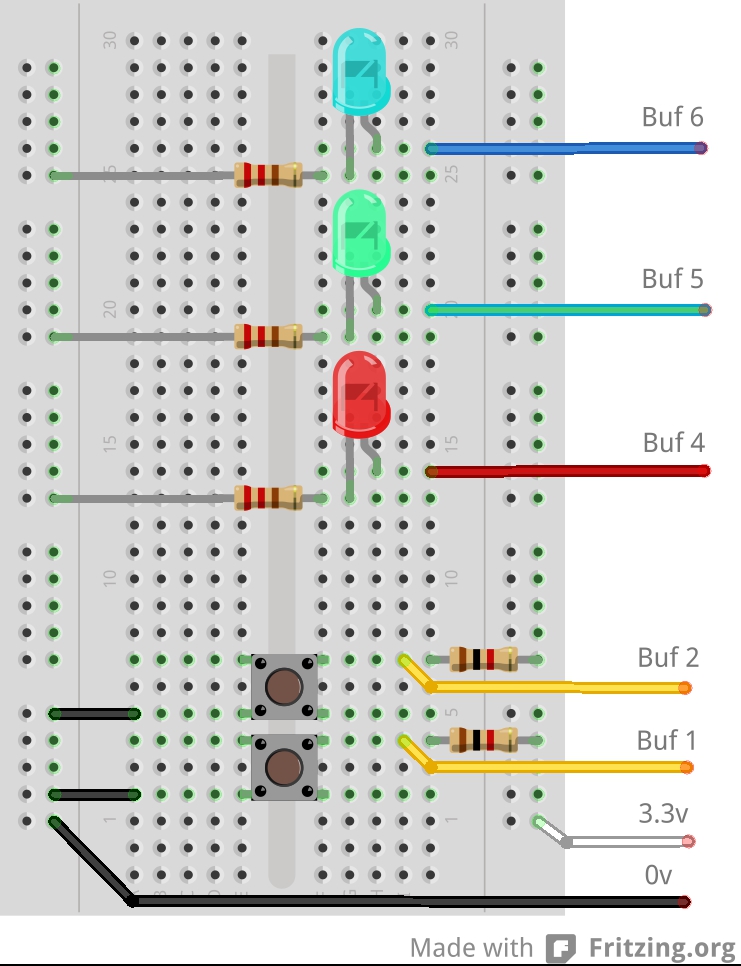
gertboard-out1In this image there are 3 LEDs connected to the Buffer pins Buf4, Buf5 and Buf6, and 2 buttons connected to Buf1 and Buf2. The first 2 buffer Input/Output jumpers have been moved to the input side. The 2 switches have pull-up resistors to the +3.3v line – this is required to stop the inputs to the 74×244 buffer chips from floating when the switch isn’t pushed. The switches connect the input to 0v when pushed – so like the on-board buttons they read high, or logic 1 when not pushed and low/0 when they are pushed. The breadboard picks up 3.3v and 0v from pins on the Gertboard (via the white and black wires)

I’m running same buttons.c program as before, but this time using the buttons on the breadboard to turn the external LEDs on/off – the third button on the Gertboard controls the last LED.

Note that the large RGB LEDs used here require about 80mA each, however they have their own buffer transistors which are being driven by the normal buffered outputs from the Gertboard.

An equivalent layout on the breadboard is shown below:

gertboard1_bbSummary

  • The external buffered pins (Buf X) are just like the Pi’s own GPIO pins, but they go via a buffer which can help protect the Pi from mis-use.
  • Inputs do not have any pull-up’s or pull-down’s so we need to provide this, if required.
  • Remember to move the buffer Input/Output jumpers to the appropriate side of the 74×244 buffer chips when using the external Buf X pins on the Gertboard.

Next we’ll look at some of the higher powered outputs available on the Gertboard.

Comments

Connecting to the Gertboard — 5 Comments

  1. Couldn’t post in the High Current driver section
    Hi Gordon,
    I am having some issues trying to get the above to work with GertBoard. So I have gone back to basics. I have 2 LEDs each being driven by wiringPi pins 0 and 1 ( from buf 1 and 2). One of the LED’s is then connected to ground on the gertboard and the other connected to RLY1 on the ULN2803 (J12). I am switching both LEDs on and Off. One via the ULN (i.e WiringPi pin 0 high all the time)and switching the ULN high/low. With the other LED I am using WiringPi pin 1 High and LOW. Everything works except the ULN switched LED is very dull when on. ( Leds and resisitors are same). This is what is causing my 7 segdisplay not to work (there is not enough pwr to light). Could you give any clues as why this is so dull? Thanks again

    • Hi,

      How are you wiring the LED to the uln2803? It’s an open-collector output, so you should be wiring it from +3.3v (or +5v, or any external supply) via the LED + resistor, then to the RLY pin at the edge of the board.

      So connect:
      B17 -> B1 -> OutputBuf -> Buf1 -> Rly1
      and
      B18 -> B2 -> OutputBuf -> Buf2 -> Rly2

      All the RPWR pins are connected together, but for this, you can ignore them. Just connect +3.3v -> LED -> Resistor -> RLY1. You’ll find 3.3v next to the BUF pins on the other side of the board.

      Note that you can connect directly from GP17 to the RLY1 pin, but going the long-way round gives you an additional LED to check your programming.

      you may want to look at this:

      https://projects.drogon.net/raspberry-pi/gertboard-and-wiringpi/higher-current-drivers/

      although it’s still a work in progress…

      -Gordon

  2. Hello Gordon,
    I read temerature with a DS18S20 direct on Raspberry on BCM GPIO 4. It works.
    Now I did the same with the Gertboard. I set a wire from GP4 to B4 and a jumper
    to B4_in.
    Then I wrote gpio mode 7 in.
    But nothing is happen. WiringPi 7 is high, voltage is there, but the sensor
    didn’t make out.
    What is my failur?
    Thanks for helping.
    wolfgang

    • The DS18S20 is a 1-wire bus device (not supported by wiringPi, however the kernel driver does support it).

      The 1W protocol needs to change the pin direction from output to input and back again at time-critical periods to send commands to the device and read data back from the device… As such it can’t be used through the Gertboard as the buffers there are on-way only – and you can’t change them from output to input in the timescales required (6µS!)

      So stick to connecting it direcly to the Pi – or directly to the GP4 pin on the Gertboard and not via the buffers if you need to use the Gertboard for other purposes.

      -Gordon

  3. Hallo Gordon,
    your advice is plausibly.
    I will use the GP4 on the Gertboard direct.
    Thanks a lot.
    Wolfgang